Superincreasing sequence

In mathematics, a sequence of positive real numbers 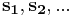\mathbf{s_1, s_2, ...} is called superincreasing if every element of the sequence is greater than the sum of all previous elements in the sequence. [1][2]

Formally, written:

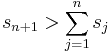
s_{n%2B1} > \sum_{j=1}^n s_j

Example

For example, (1,3,6,13,27,52) is a superincreasing sequence, but (1,3,4,9,15,25) is not.[2] The following Python source code tests a sequence of numbers to determine if it is superincreasing:

sequence = [1,3,6,13,27,52]
sum = 0
test = True
for n in sequence:
    print "Sum: ", sum, "Element: ", n
    if n <= sum: 
        test = False
        break
    sum += n
 
print "Superincreasing sequence? ", test

Produces the following output:

Sum:  0 Element:  1
Sum:  1 Element:  3
Sum:  4 Element:  6
Sum:  10 Element:  13
Sum:  23 Element:  27
Sum:  50 Element:  52
Superincreasing sequence?  True

See also

References

  1. ^ Richard A. Mollin, An Introduction to Cryptography (Discrete Mathematical & Applications), Chapman & Hall/CRC; 1 edition (August 10, 2000), ISBN 1584881275
  2. ^ a b Bruce Schneier, Applied Cryptography: Protocols, Algorithms, and Source Code in C, pages 463-464, Wiley; 2nd edition (October 18, 1996), ISBN 0471117099